ANOVA reasoning
Take a moment to check this video explaining how to calculate an ANOVA by hand…
Before we get to deep into mathematical equations, we should learn the overall idea of testing for significant differences among groups.
When you are comparing different groups of observations, you can divide the variance in the data in three different ways:
To better visualize the approach, we will keep the sum of squares and the degrees of freedom separated for each component.
- Total variance: For the Total Sum of Squares (SSt), forget that the observations belong to any group, and simply add up the difference, from each observation to the grand mean, squared. The total degrees of freedom (DFt) is the total number of observations minus one.
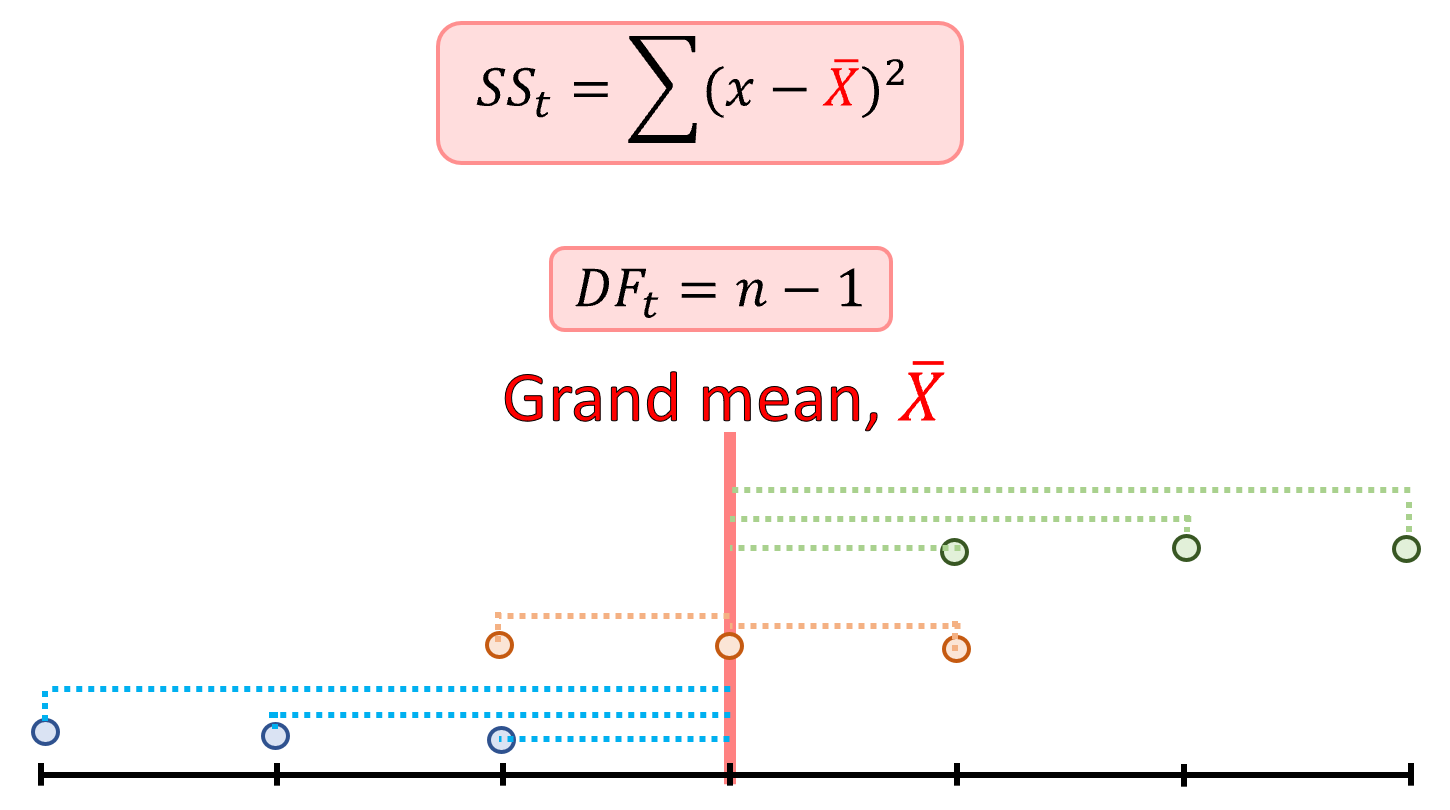
Figure 12.3: Total Sum of Squares (SSt) and total degrees of freedom (DFt)
That total variance can be now divided in the variance that occurs between and among groups:
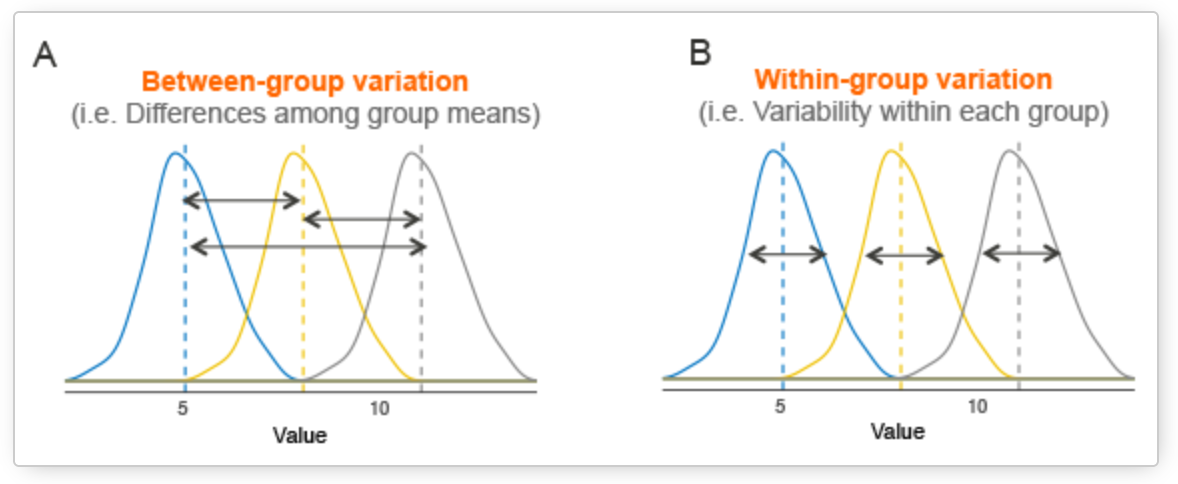
Figure 12.4: Between and within group variance
- Between groups variance: The Sum of Squares for between groups (SSb) is summation of the difference, between each group mean and the grand mean, squared and multiplied by the number of observations in each group (Formula below). The between group degrees of freedom (DFb) is the total number of groups minus one. In this case, we are only obtaining information from the groups.
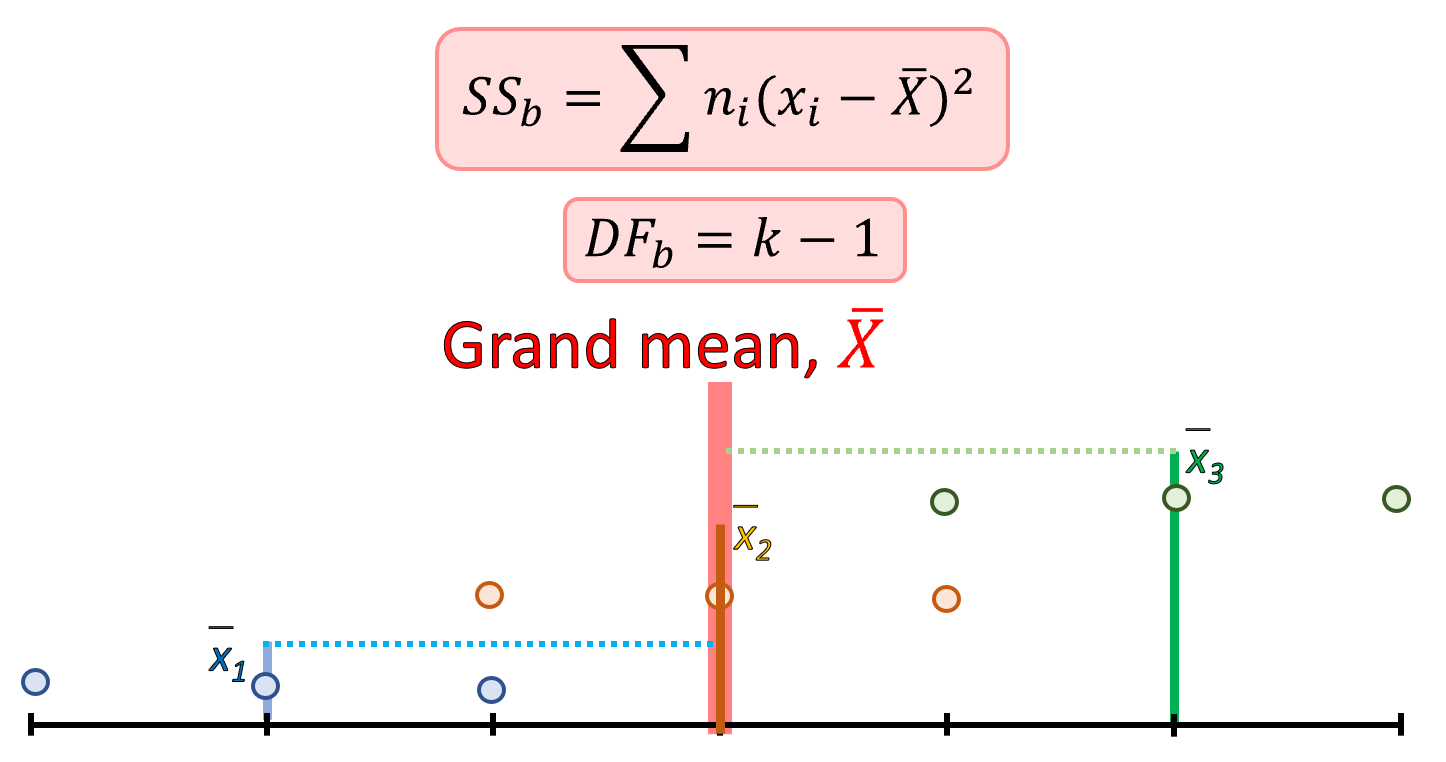
Figure 12.5: Between group variance and degrees of freedom, DF
- Within groups variance: The Sum of Squares within groups (SSw) is the summation of the difference, between each observation in a group and the mean of that group, squared. The within group degrees of freedom (DFw) is the total number of observations (n) minus the total number of groups (k).
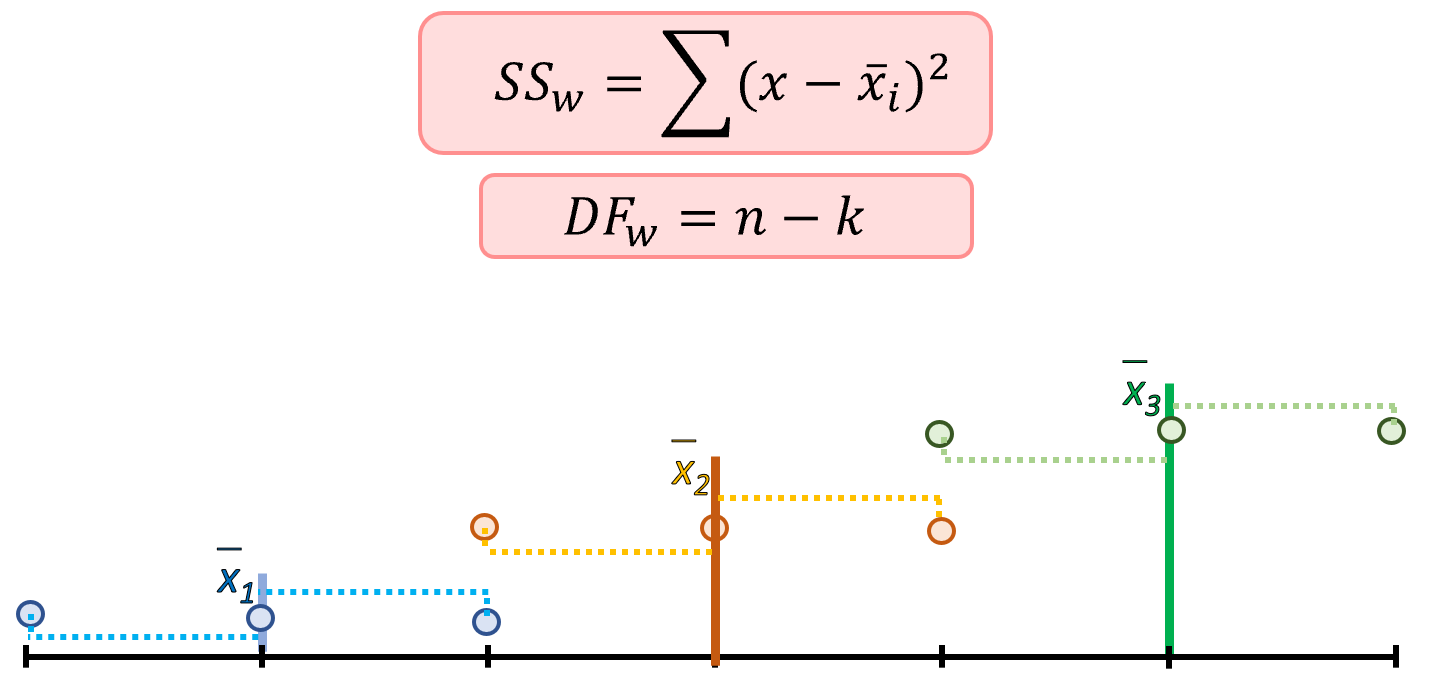
Figure 12.6: Within group variance and degrees of freedom, DF
If you take the within and between group variance and the within and between group degrees of freedom and add them up, you will get the total variance and total degrees of freedom.
The idea behind the ANOVA is to estimate the ration of the variance between groups to the variance within groups, what is also called the F-statistics, after Sir Ronald A. Fisher, who came out with this idea back in the 1920s.
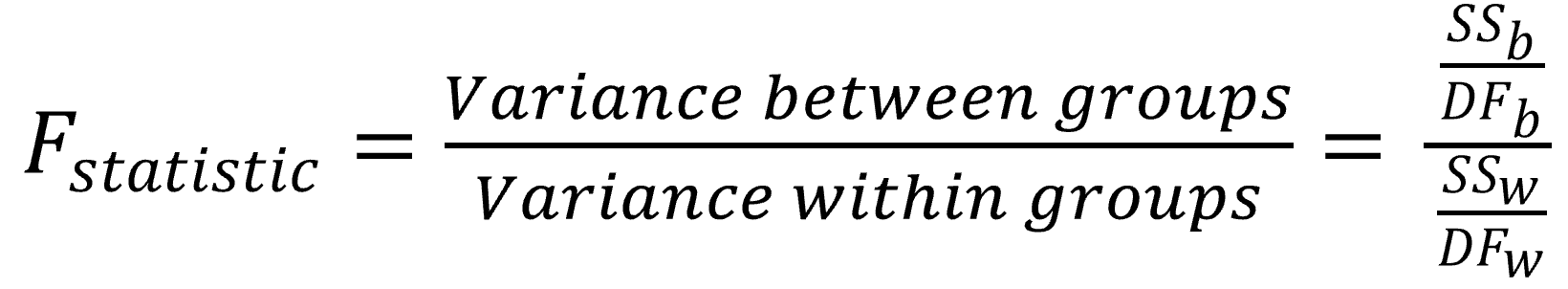
Figure 12.7: F-statistics or ratio of between group variance to within group variance
If you divide the variance between groups by the variance within groups, and the resulting F-value is smaller than one, it indicates that there are no significant differences between the means of the samples being compared.
However, a higher ratio implies that the variation among group means are greatly different from each other compared to the variation of the individual observations in each group. The variance between groups is larger than the variance within groups, so the means are likely different.
I said likely different, because you still would have to get a F-critical value, which will indicate how extreme was the F-value you calcualted.