Accepting or rejecting the null hypothesis

In a nutshell, the idea of testing a hypothesis is to see if a given individual or sample is larger or smaller than the population cutoff set by the level of significance, \(\alpha\).

In a two tail test, the null hypothesis is rejected if the sample value is larger or smaller than the critical value. On the contrary, if your sample value is within the range outlined by your critical value, then you conclude that you failed to reject the null-hypothesis. Please remember that in statistics you only “fail to reject” or “reject” the null hypothesis but you never prove the alternative hypothesis when you reject the null hypothesis.

In a right tail test, the null hypothesis is rejected if the sample value is larger than the critical value.

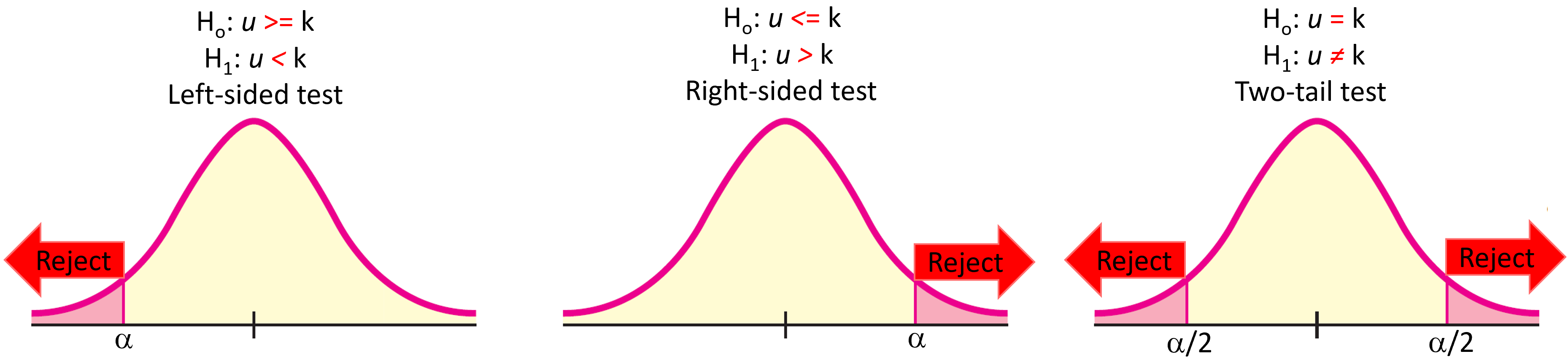
Figure 8.9: Types of tests

In a left tail test, the null hypothesis is rejected if the sample value is smaller than the critical value.

Hypotheses can also be tested by simply comparing your chosen level of significance, \(\alpha\), to your p-value. Every time your p-value is smaller than the \(\alpha\) you reject the null hypothesis.

Figure 8.10: If the P is low, the Ho must go

Think about this for a moment.

Let’s say I am testing if the heart rate of a person is significantly larger that the average population using a level of significance at 0.05.

In this case, I am assuming a heart rate will be significantly larger for any heart rate faster than the top 5% of all hearth rates in the human population.

Let’s say I measured the hearth rate of a person and estimated that it has a p-value of 0.02.

This means that the heart rate of this one person is as fast as the top 2% fastest hearth rates in the population.

In this case, the p-value is smaller than \(\alpha\), so I reject the null hypothesis, and conclude that indeed the hearth rate of the given individual is significantly larger than expected from the average human population.

Figure 8.11: The P-value